（本小题满分13分）
已知定点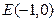
，
，动点A满足｜AE|=4，线段AF的垂直平分线交AE于点M。
（1）求点M的轨迹C1的方程；
（2）抛物线C2：
与C1在第一象限交于点P，直线PF交抛物线于另一个点Q，求抛物线的POQ弧上的点R到直线PQ的距离的最大值。
若非
是
的充分不必要条件，求
的取值范围．
i(
)，且(1+3i)z为纯虚数．
；
=
，求复数
．
是等差数列
的前
项和，且
．
；
，计算
和
，由此推测数列
是等差数列还是等比数列，证明你的结论．
求实数a的取值范围相关知识点
推荐套卷
（本小题满分13分）
已知定点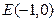，，动点A满足｜AE|=4，线段AF的垂直平分线交AE于点M。
（1）求点M的轨迹C1的方程；
（2）抛物线C2：与C1在第一象限交于点P，直线PF交抛物线于另一个点Q，求抛物线的POQ弧上的点R到直线PQ的距离的最大值。
粤公网安备 44130202000953号