本小题满分14分)
已知椭圆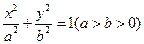 的左、右焦点分别为F1、F2,若以F2为圆心,b-c为半径作圆F2,过椭圆上一点P作此圆的切线,切点为T,且
的左、右焦点分别为F1、F2,若以F2为圆心,b-c为半径作圆F2,过椭圆上一点P作此圆的切线,切点为T,且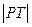 的最小值不小于
的最小值不小于 。
。
(1)证明 :椭圆上的点到F2的最短距离为
:椭圆上的点到F2的最短距离为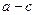 ;
;
(2)求椭圆的离心率e的取值范围;
(3)设椭圆的短半轴长为1,圆F2与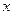 轴的右交点为Q,过点Q作斜率为
轴的右交点为Q,过点Q作斜率为 的直线
的直线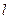 与椭圆相交于A、B两点,若OA⊥OB,求直线
与椭圆相交于A、B两点,若OA⊥OB,求直线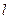 被圆F2截得的弦长S的最大值。
被圆F2截得的弦长S的最大值。
推荐套卷
本小题满分14分)
已知椭圆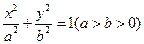 的左、右焦点分别为F1、F2,若以F2为圆心,b-c为半径作圆F2,过椭圆上一点P作此圆的切线,切点为T,且
的左、右焦点分别为F1、F2,若以F2为圆心,b-c为半径作圆F2,过椭圆上一点P作此圆的切线,切点为T,且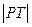 的最小值不小于
的最小值不小于 。
。
(1)证明 :椭圆上的点到F2的最短距离为
:椭圆上的点到F2的最短距离为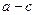 ;
;
(2)求椭圆的离心率e的取值范围;
(3)设椭圆的短半轴长为1,圆F2与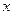 轴的右交点为Q,过点Q作斜率为
轴的右交点为Q,过点Q作斜率为 的直线
的直线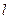 与椭圆相交于A、B两点,若OA⊥OB,求直线
与椭圆相交于A、B两点,若OA⊥OB,求直线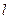 被圆F2截得的弦长S的最大值。
被圆F2截得的弦长S的最大值。