:如图,两个工厂 相距
相距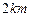 ,点
,点 为
为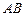 的中点,现要在以
的中点,现要在以 为圆心,
为圆心,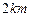 为半径的圆弧
为半径的圆弧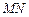 上的某一点
上的某一点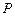 处建一幢办公楼,其中
处建一幢办公楼,其中 .据测算此办公楼受工厂
.据测算此办公楼受工厂 的“噪音影响度”与距离
的“噪音影响度”与距离 的平方成反比,比例系数是1,办公楼受工厂
的平方成反比,比例系数是1,办公楼受工厂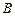 的“噪音影响度” 与距离
的“噪音影响度” 与距离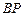 的平方也成反比,比例系数是4,办公楼受
的平方也成反比,比例系数是4,办公楼受 两厂的“总噪音影响度”
两厂的“总噪音影响度” 是受
是受 两厂“噪音影响度”的和,设
两厂“噪音影响度”的和,设 为
为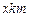 .
.
(Ⅰ)求“总噪音影响度”  关于
关于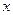 的函数关系,并求出该函数的定义域;
的函数关系,并求出该函数的定义域;
(Ⅱ)当 为多少时,“总噪音影响度”最小?
为多少时,“总噪音影响度”最小?
推荐套卷
:如图,两个工厂 相距
相距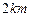 ,点
,点 为
为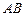 的中点,现要在以
的中点,现要在以 为圆心,
为圆心,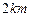 为半径的圆弧
为半径的圆弧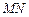 上的某一点
上的某一点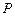 处建一幢办公楼,其中
处建一幢办公楼,其中 .据测算此办公楼受工厂
.据测算此办公楼受工厂 的“噪音影响度”与距离
的“噪音影响度”与距离 的平方成反比,比例系数是1,办公楼受工厂
的平方成反比,比例系数是1,办公楼受工厂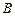 的“噪音影响度” 与距离
的“噪音影响度” 与距离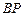 的平方也成反比,比例系数是4,办公楼受
的平方也成反比,比例系数是4,办公楼受 两厂的“总噪音影响度”
两厂的“总噪音影响度” 是受
是受 两厂“噪音影响度”的和,设
两厂“噪音影响度”的和,设 为
为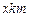 .
.
(Ⅰ)求“总噪音影响度”  关于
关于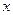 的函数关系,并求出该函数的定义域;
的函数关系,并求出该函数的定义域;
(Ⅱ)当 为多少时,“总噪音影响度”最小?
为多少时,“总噪音影响度”最小?