（本小题满分14分）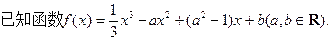
（Ⅰ）若x=1为f（x）的极值点，求a的值；
（Ⅱ）若y= f（x）的图象在点（1，f（1））处的切线方程为x+y-3=0，求f（x）在区间[-2
，4]上的最大值；
（Ⅲ
）当a≠0时，若f（x）在区间（-1，1）上不单调，求a的取值范围.
相关试题
是定义域为R上的奇函数。
的解集；
上的最小值为—2，求m的值。
上是减函数，在
（0，1）上是增函数，函数
在R上有三个零点，且1是其中一个零点。
的取值范围。
的最小正周期和单调递减区间；
上恒成立，求实数
的取值范围。
的定义域为集合A，关于x的不等式
的解集为B，求使
的取值范围。
—5：不等式选讲
的图像；
恒成立，求实数
的范围。推荐套卷
（本小题满分14分）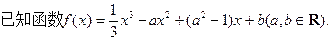
（Ⅰ）若x=1为f（x）的极值点，求a的值；
（Ⅱ）若y= f（x）的图象在点（1，f（1））处的切线方程为x+y-3=0，求f（x）在区间[-2，4]上的最大值；
（Ⅲ）当a≠0时，若f（x）在区间（-1，1）上不单调，求a的取值范围.
粤公网安备 44130202000953号