(本小题共12分)
已知椭圆E: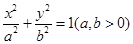 的焦点坐标为
的焦点坐标为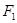 (
(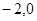 ),点M(
),点M(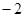 ,
,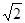 )在椭圆E上.
)在椭圆E上.
(Ⅰ)求椭圆E的方程;
(Ⅱ)设Q(1,0),过Q点引直线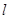 与椭圆E交于
与椭圆E交于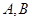 两点,求线段
两点,求线段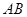 中点
中点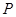 的轨迹方程;
的轨迹方程;
(Ⅲ)O为坐标原点,⊙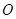 的任意一条切线与椭圆E有两个交点
的任意一条切线与椭圆E有两个交点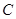 ,
, 且
且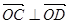 ,求⊙
,求⊙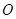 的半径.
的半径.
推荐套卷
(本小题共12分)
已知椭圆E: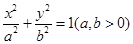 的焦点坐标为
的焦点坐标为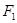 (
(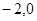 ),点M(
),点M(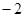 ,
,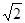 )在椭圆E上.
)在椭圆E上.
(Ⅰ)求椭圆E的方程;
(Ⅱ)设Q(1,0),过Q点引直线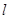 与椭圆E交于
与椭圆E交于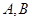 两点,求线段
两点,求线段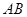 中点
中点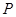 的轨迹方程;
的轨迹方程;
(Ⅲ)O为坐标原点,⊙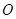 的任意一条切线与椭圆E有两个交点
的任意一条切线与椭圆E有两个交点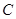 ,
, 且
且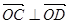 ,求⊙
,求⊙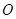 的半径.
的半径.