一次数学考试共有10道选择题,每道选择题都有4个选项,其中有且只有一个选项是正确的.设计试卷时,安排前n道题使考生都能得出正确答案,安排8-n道题,每题得出正确答案的概率为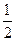 ,安排最后两道题,每题得出正确答案的概率为
,安排最后两道题,每题得出正确答案的概率为 ,且每题答对与否相互独立,同时规定:每题选对得5分,不选或选错得0分.
,且每题答对与否相互独立,同时规定:每题选对得5分,不选或选错得0分.
(1)当n=6时,
①分别求考生10道题全答对的概率和答对8道题的概率;
②问:考生答对几道题的概率最大,并求出最大值;
(2)要使考生所得分数的期望不小于40分,求n的最小值.
推荐套卷
一次数学考试共有10道选择题,每道选择题都有4个选项,其中有且只有一个选项是正确的.设计试卷时,安排前n道题使考生都能得出正确答案,安排8-n道题,每题得出正确答案的概率为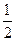 ,安排最后两道题,每题得出正确答案的概率为
,安排最后两道题,每题得出正确答案的概率为 ,且每题答对与否相互独立,同时规定:每题选对得5分,不选或选错得0分.
,且每题答对与否相互独立,同时规定:每题选对得5分,不选或选错得0分.
(1)当n=6时,
①分别求考生10道题全答对的概率和答对8道题的概率;
②问:考生答对几道题的概率最大,并求出最大值;
(2)要使考生所得分数的期望不小于40分,求n的最小值.