（满分20分）本题有2小题，第1小题12分，第2小题8分．
已知数列{
}和{
}满足：对于任何
，有
，
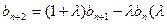为非零常数），且
．
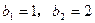（1）求数列{}和{}的通项公式；
（2）若
是
与
的等差中项，试求
的值，并研究：对任意的，是否一定能是数列{}中某两项（不同于）的等差中项，并证明你的结论．
并且与曲线
相切的直线方程。
中，满足
,
是
边上的一点.
,求向量
与向量
夹角的正弦值；
，
=m (m为正常数) 且
值；
且
求
的最小值。推荐套卷
（满分20分）本题有2小题，第1小题12分，第2小题8分．
已知数列{}和{}满足：对于任何，有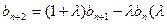，为非零常数），且．
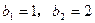（1）求数列{}和{}的通项公式；
（2）若是与的等差中项，试求的值，并研究：对任意的，是否一定能是数列{}中某两项（不同于）的等差中项，并证明你的结论．
粤公网安备 44130202000953号