(本小题满分 13分
13分 )
)
已知抛物线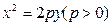 的焦点为F,过F的直线交抛物线于A、B的两点,过A、B两点分别作抛物线的切线,设其交点为M。
的焦点为F,过F的直线交抛物线于A、B的两点,过A、B两点分别作抛物线的切线,设其交点为M。
(Ⅰ )设
)设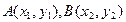 ,试用
,试用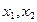 表示点M的坐标。
表示点M的坐标。
(Ⅱ) 是否为定值,如果是,请求出定
是否为定值,如果是,请求出定 值,如果不是,请说明理由。
值,如果不是,请说明理由。
(III)设△ABM的面积为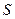 ,试确定
,试确定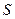 的最小值。
的最小值。
相关知识点
推荐套卷
(本小题满分 13分
13分 )
)
已知抛物线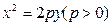 的焦点为F,过F的直线交抛物线于A、B的两点,过A、B两点分别作抛物线的切线,设其交点为M。
的焦点为F,过F的直线交抛物线于A、B的两点,过A、B两点分别作抛物线的切线,设其交点为M。
(Ⅰ )设
)设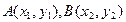 ,试用
,试用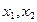 表示点M的坐标。
表示点M的坐标。
(Ⅱ) 是否为定值,如果是,请求出定
是否为定值,如果是,请求出定 值,如果不是,请说明理由。
值,如果不是,请说明理由。
(III)设△ABM的面积为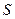 ,试确定
,试确定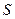 的最小值。
的最小值。