(本 小题满分14分)
小题满分14分)
已知定义在 的函数
的函数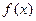 同时满足以下三条:①对任意的
同时满足以下三条:①对任意的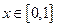 ,总有
,总有 ;②
;② ;③当
;③当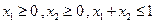 时,总有
时,总有 成立.
成立.
(1)函数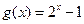 在区间
在区间 上是否同时适合①②③?并说明理由;
上是否同时适合①②③?并说明理由;
(2)设 ,且
,且 ,试比较
,试比较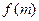 与
与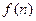 的大小;
的大小;
(3)假设存在 ,使得
,使得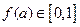 且
且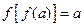 ,求证:
,求证: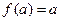 .
.
相关知识点
推荐套卷
(本 小题满分14分)
小题满分14分)
已知定义在 的函数
的函数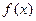 同时满足以下三条:①对任意的
同时满足以下三条:①对任意的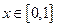 ,总有
,总有 ;②
;② ;③当
;③当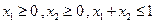 时,总有
时,总有 成立.
成立.
(1)函数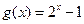 在区间
在区间 上是否同时适合①②③?并说明理由;
上是否同时适合①②③?并说明理由;
(2)设 ,且
,且 ,试比较
,试比较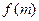 与
与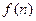 的大小;
的大小;
(3)假设存在 ,使得
,使得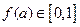 且
且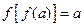 ,求证:
,求证: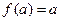 .
.