(本小题满分12分）
已知点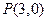
，点A、B分别在x轴负半轴和y轴上，且
，点
满足
，当点B在y轴上移动时，记点C的轨迹为E。
（1）求曲线E的方程；
（2）过点Q（1，0）且斜率为k的直线
交曲线E于不同的两点M、N，若D(
,0),且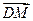
·
＞0，求k的取值范围。
的两顶点为焦点，以椭圆
，一个过点
的双曲线的长轴的端点为椭圆的焦点，求双曲线的标准方程。
，双曲线上一点
到
的距离的差的绝对值等于
，求双曲线的标准方程。
表示焦点在
轴上的双曲线，求
的范围。
的一个焦点为
，求
的值。推荐套卷
(本小题满分12分）
已知点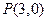，点A、B分别在x轴负半轴和y轴上，且，点满足，当点B在y轴上移动时，记点C的轨迹为E。
（1）求曲线E的方程；
（2）过点Q（1，0）且斜率为k的直线交曲线E于不同的两点M、N，若D(,0),且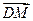·＞0，求k的取值范围。
粤公网安备 44130202000953号