某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费每满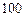 元可以
元可以
转动如图所示的圆盘一次,其中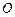 为圆心,且标有
为圆心,且标有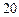 元、
元、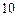 元、
元、 元的三部分区域面积相
元的三部分区域面积相
等. 假定指针停在任一位置都是等可能的.当指针停在某区域时,返相应金额的优惠券.(例
如:某顾客消费了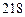 元,第一次转动获得了
元,第一次转动获得了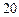 元,第二次获得了
元,第二次获得了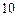 元,则其共获得了
元,则其共获得了
元 优惠券.)顾客甲和乙都到商场进行了消费,并按照规则参与了活动.
优惠券.)顾客甲和乙都到商场进行了消费,并按照规则参与了活动.
⑴若顾客甲消费了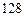 元,求他获得优惠券面额大于
元,求他获得优惠券面额大于 元的概率?
元的概率?
⑵若顾客乙消费了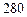 元,求他
元,求他 总共获得优惠券金额不低于
总共获得优惠券金额不低于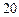 元的概率?
元的概率?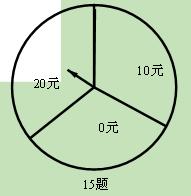
推荐套卷

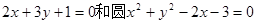 相交于点A、B,
相交于点A、B,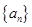 满足:
满足: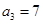 ,
, ,
,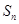 .
.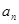 及
及
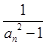 (n
(n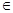 N*),求数列
N*),求数列 的前n项和
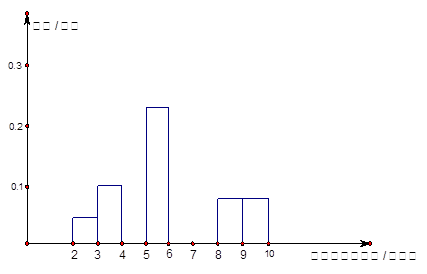
的前n项和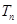 .
.
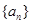 、
、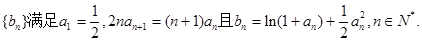
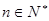 ,证明:
,证明: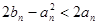 成立;
成立;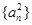 、
、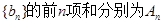 、
、
 粤公网安备 44130202000953号
粤公网安备 44130202000953号