本小题满分14分）
定义运算
，记函数
（Ⅰ）已知
，且
，求
的值；
（Ⅱ）在给定的直角坐标系中，用“五点法”作出函数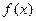
在
一个周期内的简图；
（Ⅲ）求函数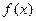的对称中心、最大值及相应的
值.
相关试题
是方程
的两根
的值（II）求
的值
最小正周期和单调增区间
时，求函数
的值域。
满足：（1）
，（2）被
轴截得的弦长为2，（3）在
轴截距为6，求此函数解析式。
≤1的解集
。
的直径
，
为圆周上一点，
，过
，过
作
，垂足为
，求∠DAC
相关知识点
推荐套卷
本小题满分14分）
定义运算，记函数
（Ⅰ）已知，且，求的值；
（Ⅱ）在给定的直角坐标系中，用“五点法”作出函数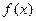在
一个周期内的简图；
（Ⅲ）求函数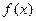的对称中心、最大值及相应的值.
粤公网安备 44130202000953号