(本小题满分14分)
如图,设抛物线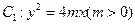 的准线与
的准线与 轴交于
轴交于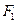 ,焦点为
,焦点为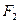 ;以
;以 为焦点,离心率
为焦点,离心率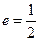 的椭圆
的椭圆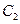 与抛物线
与抛物线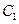 在
在 轴上方的交点为
轴上方的交点为 ,延长
,延长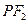 交抛物线于点
交抛物线于点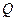 ,
,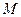 是抛物线
是抛物线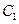 上一动点,且M在
上一动点,且M在 与
与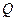 之间运动.
之间运动.
(1)当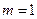 时,求椭圆
时,求椭圆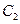 的方程,
的方程,
(2)当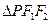 的边长恰好是三个连续的自然数时,
的边长恰好是三个连续的自然数时,
求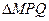 面积的最大值.
面积的最大值.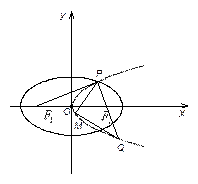
相关知识点
推荐套卷
(本小题满分14分)
如图,设抛物线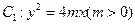 的准线与
的准线与 轴交于
轴交于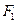 ,焦点为
,焦点为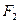 ;以
;以 为焦点,离心率
为焦点,离心率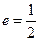 的椭圆
的椭圆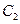 与抛物线
与抛物线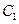 在
在 轴上方的交点为
轴上方的交点为 ,延长
,延长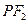 交抛物线于点
交抛物线于点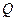 ,
,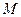 是抛物线
是抛物线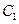 上一动点,且M在
上一动点,且M在 与
与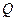 之间运动.
之间运动.
(1)当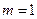 时,求椭圆
时,求椭圆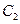 的方程,
的方程,
(2)当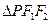 的边长恰好是三个连续的自然数时,
的边长恰好是三个连续的自然数时,
求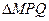 面积的最大值.
面积的最大值.