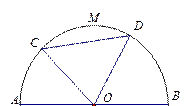
(本小题满分13分)某园林公司计划在一块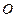 为圆心,半径为5的半圆形(如图)地上种植花草树木,其中弓形
为圆心,半径为5的半圆形(如图)地上种植花草树木,其中弓形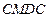 区域用于观赏样板地,
区域用于观赏样板地,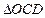 区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.
区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.
(1) 设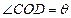 ,
,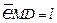 ,分别用
,分别用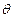 ,
,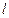 表示弓形
表示弓形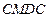 的面积
的面积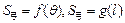 ;
;



|
 (2) 园林公司应该怎样规划这块土地,才能使总利润最大?(参考公式:扇形面积公式
(2) 园林公司应该怎样规划这块土地,才能使总利润最大?(参考公式:扇形面积公式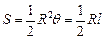 )
)
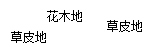 |
推荐套卷
(本小题满分13分)某园林公司计划在一块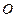 为圆心,半径为5的半圆形(如图)地上种植花草树木,其中弓形
为圆心,半径为5的半圆形(如图)地上种植花草树木,其中弓形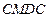 区域用于观赏样板地,
区域用于观赏样板地,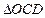 区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.
区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.
(1) 设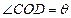 ,
,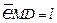 ,分别用
,分别用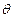 ,
,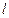 表示弓形
表示弓形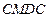 的面积
的面积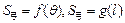 ;
;




|
 (2) 园林公司应该怎样规划这块土地,才能使总利润最大?(参考公式:扇形面积公式
(2) 园林公司应该怎样规划这块土地,才能使总利润最大?(参考公式:扇形面积公式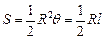 )
)
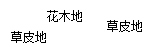 |