如图，在等腰梯形ABCD中，AB∥DC，AD=BC=5cm，AB=12cm，CD=6cm，点Q从C开始沿CD边向D移动，速度是每秒1厘米，点P从A开始沿AB向B移动，速度是点Q速度的a倍，如果点P，Q分别从A，C同时出发，当其中一点到达终点时运动停
止．设运动时间为t秒．已知当t=
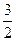时，四边形APQD是平行四边形．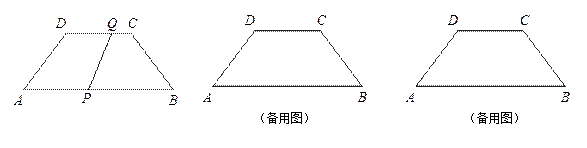
（1）求a的值；
（2
）线段PQ是否可能平分对角线BD？若能，求t的值，若不能，请说
明理由；
（3）若在某一时刻点P恰好在DQ的垂直平分线上，求此时t的值．
相关试题
已知二次函数 ，
①当 时，求这个二次函数的对称轴的方程；
②若 ，问： 为何值时，二次函数的图象与 轴相切？
③若二次函数的图象与 轴交于点 ， ， ， ，且 ， ，与 轴的正半轴交于点 ，以 为直径的半圆恰好过点 ，二次函数的对称轴 与 轴、直线 、直线 分别交于点 、 、 ，且满足 ，求二次函数的表达式．
如图所示， 的直角顶点 在函数 的图象上，顶点 、 在函数 的图象上， 轴，连接 ， ，记 的面积为 ， 的面积为 ，设 ．
①求 的值以及 关于 的表达式；
②若用 和 分别表示函数 的最大值和最小值，令 ，其中 为实数，求 ．
如图示一架水平飞行的无人机 的尾端点 测得正前方的桥的左端点 的
俯角为 其中 ，无人机的飞行高度 为 米，桥的长度为1255米．
①求点 到桥左端点 的距离；
②若无人机前端点 测得正前方的桥的右端点 的俯角为 ，求这架无人机的长度 ．
相关知识点
推荐套卷
粤公网安备 44130202000953号