(本题满分12分) 已知函数
为
上的连续函数
(Ⅰ) 若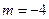
,判断
在
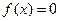上是否有零根存在?没有,请说明理由;若有,并在精确度为
的条件下(即根所在区间长度小于),用二分法求出使这个零根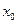
存在的小区间;
(Ⅱ)若函数
在区间
上存在零点,求实数
的取值范围.
推荐套卷
(本题满分12分) 已知函数为上的连续函数
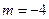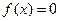(Ⅰ) 若,判断在上是否有零根存在?没有,请说明理由;若有,并在精确度为的条件下(即根所在区间长度小于),用二分法求出使这个零根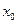存在的小区间;
(Ⅱ)若函数在区间上存在零点,求实数的取值范围.
粤公网安备 44130202000953号