(本题满分12分)
(Ⅰ)从
名男生和
名女生中任选人去参加培训,用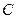
表示事件“其中至少有一名女生”，写出从中选取两人的所有可能取法和事件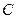的对立事件，并求事件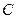的概率;
(Ⅱ)函数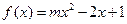
,那么任意
,使函数
在实数集上有零根的概率.
对一切实数
都有
成立,且
,(1)求
的值；(2)求 
,
,
,
,求
的值.
3,求
的值; 
，且
．
在
上的单调性，并给予证明；
. 
的奇偶性；推荐套卷
(本题满分12分)
(Ⅰ)从名男生和名女生中任选人去参加培训,用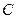表示事件“其中至少有一名女生”，写出从中选取两人的所有可能取法和事件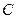的对立事件，并求事件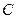的概率;
(Ⅱ)函数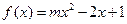,那么任意,使函数在实数集上有零根的概率.
粤公网安备 44130202000953号