已知函数 (
( ,
, ,
,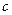 为常数,
为常数, ).
).
(Ⅰ)若 时,数列
时,数列 满足条件:点
满足条件:点 在函数
在函数 的图象上,求
的图象上,求 的前
的前 项和
项和 ;
;
(Ⅱ)在(Ⅰ)的条件下,若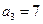 ,
, ,
, (
( ),
),
证明: ;
;
(Ⅲ)若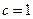 时,
时,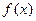 是奇函数,
是奇函数, ,数列
,数列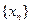 满足
满足 ,
,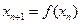 ,
,
求证: .
.
推荐套卷
已知函数 (
( ,
, ,
,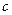 为常数,
为常数, ).
).
(Ⅰ)若 时,数列
时,数列 满足条件:点
满足条件:点 在函数
在函数 的图象上,求
的图象上,求 的前
的前 项和
项和 ;
;
(Ⅱ)在(Ⅰ)的条件下,若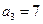 ,
, ,
, (
( ),
),
证明: ;
;
(Ⅲ)若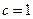 时,
时,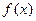 是奇函数,
是奇函数, ,数列
,数列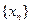 满足
满足 ,
,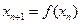 ,
,
求证: .
.