(本小题满分16分)
给定两个长度为1的平面向量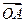 和
和 ,它们的夹角为
,它们的夹角为 .
.
(1)求|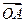 +
+ |;
|;
(2)如图(1)所示,点 在以
在以 为圆心的圆弧⌒AB上运动.若
为圆心的圆弧⌒AB上运动.若
其中 ,求
,求 的最大值?
的最大值?
(3)若点 、点
、点 在以
在以 为圆心,1为半径的圆上,且
为圆心,1为半径的圆上,且 ,问
,问 与
与 的夹角
的夹角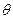 取何值时,
取何值时, 的值最大?并求出这个最大值.
的值最大?并求出这个最大值.
图(1) 图(2)
推荐套卷
(本小题满分16分)
给定两个长度为1的平面向量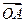 和
和 ,它们的夹角为
,它们的夹角为 .
.
(1)求|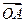 +
+ |;
|;
(2)如图(1)所示,点 在以
在以 为圆心的圆弧⌒AB上运动.若
为圆心的圆弧⌒AB上运动.若
其中 ,求
,求 的最大值?
的最大值?
(3)若点 、点
、点 在以
在以 为圆心,1为半径的圆上,且
为圆心,1为半径的圆上,且 ,问
,问 与
与 的夹角
的夹角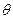 取何值时,
取何值时, 的值最大?并求出这个最大值.
的值最大?并求出这个最大值.
图(1) 图(2)