已知以点C (t,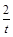 
)（t∈R），t≠0）为圆心的圆与x轴交于点O，A，与y轴交于点O，B，其中O为坐标原点．
（1）求证：△OAB的面积为定值；
（2）设直线y= –2x+4与圆C交于点M，N若|OM|=|ON|，求圆C的方程．
（3）若t＞0，当圆C的半径最小时，圆C上至少有三个不同的点到直线l：y –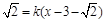
的距离为
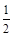，求直线l的斜率k的取值范围．
相关试题
和
的图象关于y轴对称,且
;
对一切实数
均有
成立，
.
的值；
恒成立时，求
的取值范围
中，已知
，
，在
.
.
.
上，分别截取
，设四边形
的面积为
.
之间的函数关系式；
和
的图象关于y轴对称,且
;
是常数,且
,满足
,且
有唯一解,求
的解析式推荐套卷
已知以点C (t, 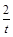)（t∈R），t≠0）为圆心的圆与x轴交于点O，A，与y轴交于点O，B，其中O为坐标原点．
（1）求证：△OAB的面积为定值；
（2）设直线y= –2x+4与圆C交于点M，N若|OM|=|ON|，求圆C的方程．
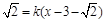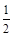（3）若t＞0，当圆C的半径最小时，圆C上至少有三个不同的点到直线l：y –的距离为，求直线l的斜率k的取值范围．
粤公网安备 44130202000953号