以下茎叶图记录了甲、乙两组各四名同学的植树棵树。乙组记录中有一个数据模糊,无法确认,在图中以X表示。
(Ⅰ)如果X=8,求乙组同学植树棵树的平均数和方差;
(Ⅱ)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵树Y的分布列和数学期望。
(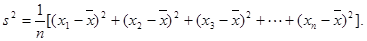 其中
其中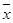 为
为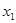 ,
,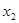 ,……
,…… 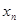 的平均数)
的平均数)
推荐套卷
以下茎叶图记录了甲、乙两组各四名同学的植树棵树。乙组记录中有一个数据模糊,无法确认,在图中以X表示。
(Ⅰ)如果X=8,求乙组同学植树棵树的平均数和方差;
(Ⅱ)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵树Y的分布列和数学期望。
(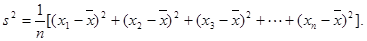 其中
其中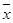 为
为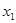 ,
,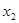 ,……
,…… 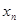 的平均数)
的平均数)