(文科做以下(1)(2)(3))
(1)、已知 ,求数列
,求数列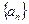 的通项公式;
的通项公式;
(2)、在(1)的条件下,数列 ,求证数列
,求证数列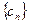 是一个 “1类和科比数列”;
是一个 “1类和科比数列”;
(3)、设等差数列 是一个 “
是一个 “ 类和科比数列”,其中首项
类和科比数列”,其中首项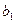 ,公差
,公差 ,探究
,探究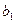
与 的数量关系,并写出相应的常数
的数量关系,并写出相应的常数 ;
;
推荐套卷
(文科做以下(1)(2)(3))
(1)、已知 ,求数列
,求数列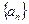 的通项公式;
的通项公式;
(2)、在(1)的条件下,数列 ,求证数列
,求证数列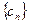 是一个 “1类和科比数列”;
是一个 “1类和科比数列”;
(3)、设等差数列 是一个 “
是一个 “ 类和科比数列”,其中首项
类和科比数列”,其中首项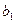 ,公差
,公差 ,探究
,探究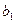
与 的数量关系,并写出相应的常数
的数量关系,并写出相应的常数 ;
;