(本题满分14分)
已知函数 ,
, ,其图象过点
,其图象过点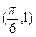
(1) 求 的解析式,并求对称中心
的解析式,并求对称中心
(2) 将函数 的图象上各点纵坐标不变,横坐标扩大为原来的2倍,然后各点横坐标不变,纵坐标扩大为原来的2倍,得到
的图象上各点纵坐标不变,横坐标扩大为原来的2倍,然后各点横坐标不变,纵坐标扩大为原来的2倍,得到 的图象,求函数
的图象,求函数 在
在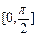 上的最大值和最小值.
上的最大值和最小值.
相关知识点
推荐套卷
(本题满分14分)
已知函数 ,
, ,其图象过点
,其图象过点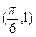
(1) 求 的解析式,并求对称中心
的解析式,并求对称中心
(2) 将函数 的图象上各点纵坐标不变,横坐标扩大为原来的2倍,然后各点横坐标不变,纵坐标扩大为原来的2倍,得到
的图象上各点纵坐标不变,横坐标扩大为原来的2倍,然后各点横坐标不变,纵坐标扩大为原来的2倍,得到 的图象,求函数
的图象,求函数 在
在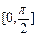 上的最大值和最小值.
上的最大值和最小值.