必做题, 本小题10分．解答时应写出文字说明、证明过程或演算步骤．
在三棱锥ABCD中，平面DBC⊥平面ABC，△ABC为正三角形， AC=2，DC=DB=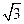
，
（1）求DC与AB所成角的余弦值；
（2）在平面ABD上求一点P，使得CP⊥平面AB D． 
相关试题
的重心
，作
面
．
和△
都是直角三角形．
中，
是
的中点，
．
；
的距离；
与平面
的位置关系，并证明你的结论．
中，
，
，
，点
在
上，且
．
平面
；
为棱，
与
为面的二面角的大小．
中，
，
，求证：
．
推荐套卷
必做题, 本小题10分．解答时应写出文字说明、证明过程或演算步骤．
在三棱锥ABCD中，平面DBC⊥平面ABC，△ABC为正三角形， AC=2，DC=DB=，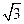
（1）求DC与AB所成角的余弦值；
（2）在平面ABD上求一点P，使得CP⊥平面AB D．
粤公网安备 44130202000953号