舰A在舰B的正东6千米处，舰C在舰B的北偏西30°且与B相距4千米，它们准备捕海洋动物，某时刻A发现动物信号，4秒后B、C同时发现这种信号，A发射麻醉炮弹.设舰与动物均为静止的，动物信号的传播速度为1千米/秒，炮弹的速度是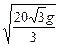
千米/秒，其中g为重力加速度，若不计空气阻力与舰高，问舰A发射炮弹的方位角和仰角应是多少？
相关试题
，
，
，
，试求两个目标物Ｍ，Ｎ之间的距离.
中，E、F、G分别为
、
、
的中点，O为
与
的交点，
面
与平面
和
的交点且与直线
垂直的直线方程.
，
,求
.
为坐标原点，
为椭圆
在
轴正半轴上的焦点，过
的直线
与
交与
、
两点，点
满足
，证明：相关知识点
推荐套卷
舰A在舰B的正东6千米处，舰C在舰B的北偏西30°且与B相距4千米，它们准备捕海洋动物，某时刻A发现动物信号，4秒后B、C同时发现这种信号，A发射麻醉炮弹.设舰与动物均为静止的，动物信号的传播速度为1千米/秒，炮弹的速度是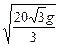千米/秒，其中g为重力加速度，若不计空气阻力与舰高，问舰A发射炮弹的方位角和仰角应是多少？
粤公网安备 44130202000953号