（本小题满分12分）
某学生在上学路上要经过4个路口，假设在各路口是否遇到红灯是相互独立的，遇到红灯的概率都是
，遇到红灯时停留的时间都是
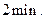
（Ⅰ）求这名学生在上学路上到第三个路口时首次遇到红灯的概率；
（Ⅱ）这名学生在上学路上因遇到红灯停 留的总时间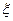
的分布列及期望
，试求 
的值．
．
，求
；
的夹角为60°，求
；
，求
，且A为锐角.
的值域.
,求
的值；
求
的夹角。
的前
项的和为
,且
，求：
的通项公式
及前
推荐套卷
（本小题满分12分）
某学生在上学路上要经过4个路口，假设在各路口是否遇到红灯是相互独立的，遇到红灯的概率都是，遇到红灯时停留的时间都是
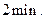
（Ⅰ）求这名学生在上学路上到第三个路口时首次遇到红灯的概率；
（Ⅱ）这名学生在上学路上因遇到红灯停 留的总时间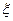的分布列及期望
粤公网安备 44130202000953号