(本试卷共40分,考试时间30分钟)
21.(选做题)本大题包括A,B,C,D共4小题,请从这4题中选做2小题. 每小题10分,共20分.请在答题卡上准确填涂题目标记. 解答时应写出文字说明、证明过程或演算步骤.
A. 选修4-1:几何证明选讲
如图,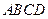 是边长为
是边长为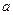 的正方形,以
的正方形,以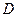 为圆心,
为圆心,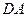 为半径的圆弧与以
为半径的圆弧与以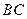 为直径的半⊙O交于点
为直径的半⊙O交于点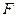 ,延长
,延长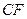 交
交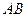 于
于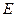 .
.
(1)求证: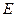 是
是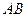 的中点;(2)求线段
的中点;(2)求线段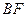 的长.
的长.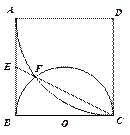
相关知识点
推荐套卷
(本试卷共40分,考试时间30分钟)
21.(选做题)本大题包括A,B,C,D共4小题,请从这4题中选做2小题. 每小题10分,共20分.请在答题卡上准确填涂题目标记. 解答时应写出文字说明、证明过程或演算步骤.
A. 选修4-1:几何证明选讲
如图,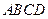 是边长为
是边长为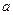 的正方形,以
的正方形,以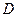 为圆心,
为圆心,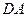 为半径的圆弧与以
为半径的圆弧与以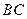 为直径的半⊙O交于点
为直径的半⊙O交于点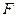 ,延长
,延长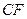 交
交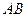 于
于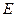 .
.
(1)求证: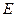 是
是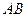 的中点;(2)求线段
的中点;(2)求线段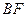 的长.
的长.