（满分16分）
记函数f(x)的定义域为D，若存在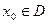
，使
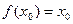成立，则称以
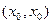为坐标的点为函数
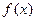图象上的不动点。
（1）若函数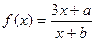
的图象上有两个关于原点对称的不动点，求
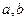应满足的条件；
（2）下述结论“若定义在Ｒ上的奇函数f(x)的图象上存在有限个不动点，则不动点有奇数个”是否正确？若正确，请给予证明，并举出一例；若不正确，请举出一反例说明
相关试题
有两个不相等的正实数根，命题q:函数
的图象与
轴无公共点;若“p且q”为真命题，求
的取值范围.
，
，
，讨论
的极值点的个数；
，求证：对任意的
，且
时，都有
满足
，求
的取值范围；
，使得集合
，如果存在，请求出
的取值范围；反之，请说明理由.
的单调区间；（II）若关于
的不等式
对一切
都成立
，求实数
的取值范围.
，
，
”是“
”的充分不必要条件，求
的取值范围.相关知识点
推荐套卷
（满分16分）
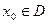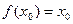记函数f(x)的定义域为D，若存在，使成立，则称以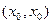为坐标的点为函数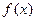图象上的不动点。
（1）若函数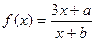的图象上有两个关于原点对称的不动点，求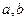应满足的条件；
（2）下述结论“若定义在Ｒ上的奇函数f(x)的图象上存在有限个不动点，则不动点有奇数个”是否正确？若正确，请给予证明，并举出一例；若不正确，请举出一反例说明
粤公网安备 44130202000953号