（本小题12分）
已知向量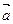
=（cos(x+
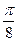），sin
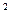(x+）），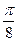
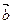=（sin(x+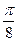），1），函数f（x）=1－2·.
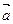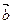（1）求函数f(x)的解析式，并求其最小正周期；
（2）求函数f(x)的单调递减区间；
（3）若方程f(x)+2m=0在[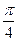
，
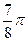]上有两个实数根，试求实数m的取值范围。
相关试题
圆
则
为何值时，
与圆
相切；
端点Q在圆
上运动，求线段PQ的中点
的轨迹方程。
且在两坐标轴上的截距的绝对值相等，求直线的方程。
中，求：
与
所成的角；
与
所成的角。
中，底面边长为
，侧棱长为
，
为棱
的中点，记以
为棱，
，
为面的二面角大小为
，
值，使直线
平面
，
与
的大小。推荐套卷
（本小题12分）
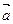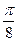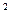已知向量=（cos(x+），sin(x+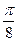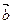）），=（sin(x+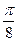），1），函数f（x）=1－2·.
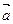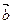（1）求函数f(x)的解析式，并求其最小正周期；
（2）求函数f(x)的单调递减区间；
（3）若方程f(x)+2m=0在[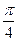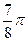，]上有两个实数根，试求实数m的取值范围。
粤公网安备 44130202000953号