(本小题满分14分)
已知函数 .
.
(Ⅰ)求证:存在定点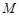 ,使得函数
,使得函数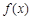 图象上任意一点
图象上任意一点 关于
关于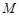 点对称的点
点对称的点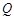 也在函数
也在函数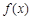 的图象上,并求出点
的图象上,并求出点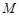 的坐标;
的坐标;
(Ⅱ)定义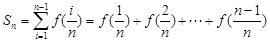 ,其中
,其中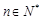 且
且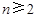 ,求
,求 ;
;
(Ⅲ)对于(Ⅱ)中的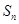 ,求证:对于任意
,求证:对于任意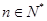 都有
都有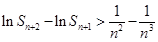 .
.
推荐套卷
(本小题满分14分)
已知函数 .
.
(Ⅰ)求证:存在定点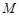 ,使得函数
,使得函数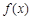 图象上任意一点
图象上任意一点 关于
关于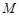 点对称的点
点对称的点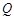 也在函数
也在函数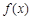 的图象上,并求出点
的图象上,并求出点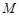 的坐标;
的坐标;
(Ⅱ)定义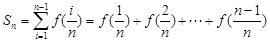 ,其中
,其中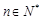 且
且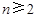 ,求
,求 ;
;
(Ⅲ)对于(Ⅱ)中的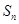 ,求证:对于任意
,求证:对于任意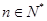 都有
都有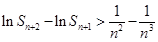 .
.