(本小题满分12分)
已知函数f(x)=4x3-3x2sin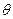
+
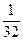的极小值大于零,其中x∈R, 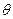∈[0,
].
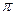(1).求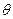的取值范围.
(2).若在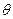的取值范围内的任意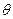,函数f(x)在区间(2a-1,a)内都是增函数,求实数a的取值范围.
(3).设x0＞
,f(x0) ＞,若f[f(x0)]=x0,求证f(x0)=x0
相关知识点
推荐套卷
(本小题满分12分)
已知函数f(x)=4x3-3x2sin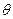+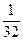的极小值大于零,其中x∈R, 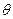∈[0,].
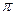(1).求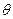的取值范围.
(2).若在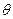的取值范围内的任意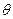,函数f(x)在区间(2a-1,a)内都是增函数,求实数a的取值范围.
(3).设x0＞,f(x0) ＞,若f[f(x0)]=x0,求证f(x0)=x0
粤公网安备 44130202000953号