已知函数
为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
（1）求
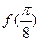的值；
（2）将函数y=f(x)的图象向右平移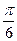
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍，纵坐标不变，得到函数y=g(x)的图象,求g(x)的单调递减区间.
相关试题
，数列
是首项为a，公比也为a的等比数列，令
，求数列
的前
项和
。
的二次项系数为
，且不等式
的解集为
，
有两个相等的实根，求
的内角A、B、C、所对的边分别为a、b、c，已知
的值.
为多面体，平面
与平面
垂直，点
在线段
上，
△OAB，,△
，△
，△
都是正三角形。
∥
；
中，角
所对的边分别为
，且满足
，
．
，求
的值．相关知识点
推荐套卷
已知函数为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
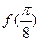（1）求的值；
（2）将函数y=f(x)的图象向右平移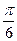个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍，纵坐标不变，得到函数y=g(x)的图象,求g(x)的单调递减区间.
粤公网安备 44130202000953号