设｛an｝是由正数组成的等差数列，Sn是其前n项和
（1）若Sn＝20，S2n＝40，求S3n的值；
（2）若互不相等正整数p，q，m，使得p＋q＝2m，证明：不等式SpSq＜S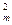
成立；
（3）是否存在常数k和等差数列｛an｝，使ka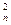
－1＝S2n－Sn+1恒成立（n∈N*），若存在，试求出常数k和数列｛an｝的通项公式；若不存在，请说明理由。
相关试题
在
上是减函数；
的最小正周期和值域；
，且
，求
的值.
的单调性；
和
，记过点
的直线的斜率为
，问：是否存在
，使得
？若存在，求出
，
，求
在
处的切线方程；（II）求
上的最小值.
为选出的4名选手中女选手的人数，求相关知识点
推荐套卷
设｛an｝是由正数组成的等差数列，Sn是其前n项和
（1）若Sn＝20，S2n＝40，求S3n的值；
（2）若互不相等正整数p，q，m，使得p＋q＝2m，证明：不等式SpSq＜S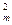成立；
（3）是否存在常数k和等差数列｛an｝，使ka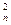－1＝S2n－Sn+1恒成立（n∈N*），若存在，试求出常数k和数列｛an｝的通项公式；若不存在，请说明理由。
粤公网安备 44130202000953号