(本小题满分12分)
已知三棱柱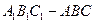 中,三个侧面均为矩形,底面
中,三个侧面均为矩形,底面 为等腰直角三角形,
为等腰直角三角形,  ,点
,点 为棱
为棱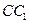 的中点,点
的中点,点 在棱
在棱 上运动.
上运动.
(1)求证

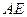 ;
;
(II)当点 运动到某一位置时,恰好使二面角
运动到某一位置时,恰好使二面角 的平面角的余弦值为
的平面角的余弦值为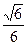 ,求点
,求点 到平面
到平面 的距离;
的距离;
(III)在(II)的条件下,试确定线段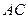 上是否存在一点
上是否存在一点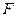 ,使得
,使得 平面
平面 ?若存在,确定其位置;若不存在,说明理由.
?若存在,确定其位置;若不存在,说明理由.
推荐套卷
(本小题满分12分)
已知三棱柱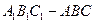 中,三个侧面均为矩形,底面
中,三个侧面均为矩形,底面 为等腰直角三角形,
为等腰直角三角形,  ,点
,点 为棱
为棱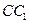 的中点,点
的中点,点 在棱
在棱 上运动.
上运动.
(1)求证

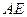 ;
;
(II)当点 运动到某一位置时,恰好使二面角
运动到某一位置时,恰好使二面角 的平面角的余弦值为
的平面角的余弦值为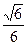 ,求点
,求点 到平面
到平面 的距离;
的距离;
(III)在(II)的条件下,试确定线段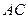 上是否存在一点
上是否存在一点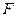 ,使得
,使得 平面
平面 ?若存在,确定其位置;若不存在,说明理由.
?若存在,确定其位置;若不存在,说明理由.