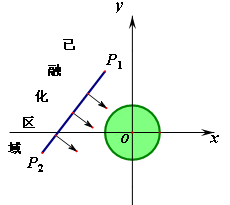
为了考察冰川融化的状况,一支科考队在某冰川上设一定一个以大本营O为圆心,半径为4km 圆形考察区域,线段P1、P2是冰川的部分边界线(不考虑其它边界),当冰川融化时,边界线沿着与其垂直的方向朝考察区域平行移动.若经过n年,冰川的边界线P1P2移动的距离为s(km),并且s与n(n为正整数)的关系是 .以O为原点,建立如图所示的平面直角坐标系,其中P1、P2的坐标分别是(–4,9)、(–13,–3).
.以O为原点,建立如图所示的平面直角坐标系,其中P1、P2的坐标分别是(–4,9)、(–13,–3).
(1)求线段P1P2所在的直线对应的函数关系式;
(2)求冰川的边界线移动到考察区域所需要的最短时间.