(本题满分14分) 已知实数a满足0<a≤2,a≠1,设函数f (x)= x3-
x3-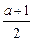 x2+ax.
x2+ax.
(Ⅰ) 当a=2时,求f (x)的极小值;
(Ⅱ) 若函数g(x)=x3+bx2-(2b+4)x+ln x (b∈R)的极小值点与f (x)的极小值点相同.求证:g(x)的极大值小于等于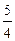 .
.
求a,b及c的值.
推荐套卷
(本题满分14分) 已知实数a满足0<a≤2,a≠1,设函数f (x)= x3-
x3-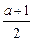 x2+ax.
x2+ax.
(Ⅰ) 当a=2时,求f (x)的极小值;
(Ⅱ) 若函数g(x)=x3+bx2-(2b+4)x+ln x (b∈R)的极小值点与f (x)的极小值点相同.求证:g(x)的极大值小于等于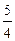 .
.
求a,b及c的值.