（本小题满分15分）如图，摄影爱好者S在某公园A处，发现正前方B处有一立柱，测得立柱顶端O的仰角和立柱底部B的俯角均为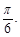
设S的眼睛距地面的距离
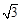米．
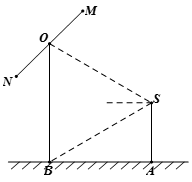
（1）求摄影者到立柱的水平距离和立柱的高度；
（2）立柱的顶端有一长2米的彩杆MN绕其中点O在S与立柱所在的平面内旋转．摄影者有一视角范围为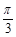
的镜头，在彩杆转动的任意时刻，摄影者是否都可以将彩杆全部摄入画面？说明理由．
相关试题
中，
，
，求角
的大小．
、
、
是同一平面内的三个向量，其中
．
，且
，求
，且
与
垂直，求
．
中，设
，
，又
，
，向量
，
的夹角为．
表示
；
是
边的中点，直线
交
于
点，求
．
的顶点在原点，始边与
轴的正半轴重合，终边经过点
．
的值；
，求函数
在区间
上的值域．
的前
项和为
，
．
的前
，
，点
在直线
上，若存在
，使不等式
成立，求实数
的最大值．推荐套卷
（本小题满分15分）如图，摄影爱好者S在某公园A处，发现正前方B处有一立柱，测得立柱顶端O的仰角和立柱底部B的俯角均为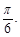设S的眼睛距地面的距离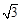米．
（1）求摄影者到立柱的水平距离和立柱的高度；
（2）立柱的顶端有一长2米的彩杆MN绕其中点O在S与立柱所在的平面内旋转．摄影者有一视角范围为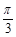的镜头，在彩杆转动的任意时刻，摄影者是否都可以将彩杆全部摄入画面？说明理由．
粤公网安备 44130202000953号