（本小题满分14分）设函数f（x）＝ln x＋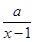
在（e，＋∞）内有极值.
（Ⅰ）求实数a的取值范围；
（Ⅱ）记g（x）＝f（x）＋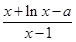
，判断g（x）的导函数g'（x）在定义域内的单调性；
（Ⅲ）若k＜f（x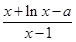）＋对任意x＞1恒成立，求整数k的最大值
相关试题
+k
)=-2cos(
;
sin2
cos2
+cos
,
).求值：
.
=2,求下列各式的值：
;
;
＜x＜0,sinx+cosx=
.
的值.推荐套卷
（本小题满分14分）设函数f（x）＝ln x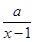＋在（e，＋∞）内有极值.
（Ⅰ）求实数a的取值范围；
（Ⅱ）记g（x）＝f（x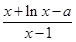）＋，判断g（x）的导函数g'（x）在定义域内的单调性；
（Ⅲ）若k＜f（x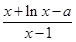）＋对任意x＞1恒成立，求整数k的最大值
粤公网安备 44130202000953号