(本小题满分14分)已知f(x)=ln(1+x)-x.
(Ⅰ)求f(x)的最大值;
(Ⅱ)数列{an}满足:an+1= 2f' (an) +2,且a1=2.5, = bn,
= bn,
⑴数列{ bn+ }是等比数列 ⑵判断{an}是否为无穷数列。
}是等比数列 ⑵判断{an}是否为无穷数列。
(Ⅲ)对n∈N*,用⑴结论证明:ln(1+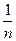 +
+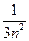 )<
)<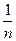 ;
;
推荐套卷
(本小题满分14分)已知f(x)=ln(1+x)-x.
(Ⅰ)求f(x)的最大值;
(Ⅱ)数列{an}满足:an+1= 2f' (an) +2,且a1=2.5, = bn,
= bn,
⑴数列{ bn+ }是等比数列 ⑵判断{an}是否为无穷数列。
}是等比数列 ⑵判断{an}是否为无穷数列。
(Ⅲ)对n∈N*,用⑴结论证明:ln(1+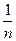 +
+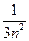 )<
)<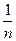 ;
;