已知Ａ、B是圆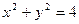
上满足条件
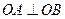的两个点，其中O是坐标原点，
分别过A、B作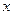
轴的垂线段，交椭圆
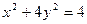于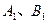
点，动点P满足
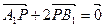.（1）求动点P的轨迹方程；（2）设S1和S2
分别表示
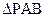和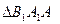
的面积，当点P在x轴的上方，点A在x轴的下方时，求
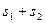的最大值。
点在以坐标轴为对称轴的椭圆上，点
和
，过
倍，且过点
，并且以坐标轴为对称轴，
表示焦点在
轴上的椭圆，求
的取值范围。
；（2）
。
的左焦点到直线
的距离为
，求椭圆的方程。推荐套卷
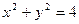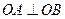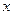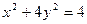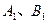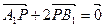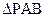已知Ａ、B是圆上满足条件的两个点，其中O是坐标原点，分别过A、B作轴的垂线段，交椭圆于点，动点P满足.（1）求动点P的轨迹方程；（2）设S1和S2分别表示和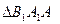的面积，当点P在x轴的上方，点A在x轴的下方时，求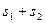的最大值。
粤公网安备 44130202000953号