本小题满分14分）如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，PA⊥平面ABCD，点M、N分别为BC、PA的中点，且PA＝AD＝2，AB＝1，AC＝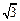
．
（Ⅰ）证明：CD⊥平面PAC；
（Ⅱ）在线段PD上是否存在一点E，使得NM∥平面ACE；若存在，求出PE的长；若不存在，说明理由．
相关试题
是二次函数，且满足
，
在
单调，求
的取值范围。
，
，当
时，求
，其中
，
（2） 求 
，且函数
在
和
处都取得极值。
的值；
，
恒成立，求实数
的取值范围。推荐套卷
本小题满分14分）如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，PA⊥平面ABCD，点M、N分别为BC、PA的中点，且PA＝AD＝2，AB＝1，AC＝．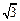
（Ⅰ）证明：CD⊥平面PAC；
（Ⅱ）在线段PD上是否存在一点E，使得NM∥平面ACE；若存在，求出PE的长；若不存在，说明理由．
粤公网安备 44130202000953号