一个如图所示的不规则形铁片,其缺口边界是口宽4分米,深2分米(顶点至两端点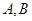 所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.
所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.
(1)若保持其缺口宽度不变,求裁剪后梯形缺口面积的最小值;
(2)若保持其缺口深度不变,求裁剪后梯形缺口面积的最小值.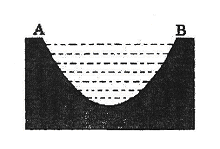
推荐套卷
一个如图所示的不规则形铁片,其缺口边界是口宽4分米,深2分米(顶点至两端点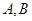 所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.
所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.
(1)若保持其缺口宽度不变,求裁剪后梯形缺口面积的最小值;
(2)若保持其缺口深度不变,求裁剪后梯形缺口面积的最小值.