(本小题满分12分)如图在棱长为1正方体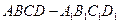 中,以正方体的三条棱所在直线为轴建立空间直角坐标系
中,以正方体的三条棱所在直线为轴建立空间直角坐标系 ,
,
(I)若点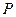 在线段
在线段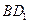 上,且满足
上,且满足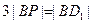 ,试写出点
,试写出点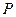 的坐标并写出
的坐标并写出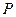 关于平面
关于平面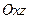 的对称点
的对称点 的坐标;
的坐标;
(Ⅱ)线段 中点为
中点为 ,求点
,求点 到点
到点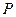 的距离。
的距离。
推荐套卷
(本小题满分12分)如图在棱长为1正方体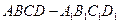 中,以正方体的三条棱所在直线为轴建立空间直角坐标系
中,以正方体的三条棱所在直线为轴建立空间直角坐标系 ,
,
(I)若点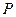 在线段
在线段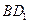 上,且满足
上,且满足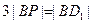 ,试写出点
,试写出点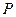 的坐标并写出
的坐标并写出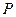 关于平面
关于平面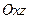 的对称点
的对称点 的坐标;
的坐标;
(Ⅱ)线段 中点为
中点为 ,求点
,求点 到点
到点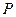 的距离。
的距离。