(本题12分)已知函数f (x)=x 2+ax ,且对任意的实数x都有f (1+x)=f (1-x) 成立.
(1)求实数 a的值;
(2)利用单调性的定义证明函数f(x)在区间[1,+∞ 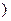 上是增函数.
上是增函数.
相关知识点
推荐套卷
(本题12分)已知函数f (x)=x 2+ax ,且对任意的实数x都有f (1+x)=f (1-x) 成立.
(1)求实数 a的值;
(2)利用单调性的定义证明函数f(x)在区间[1,+∞ 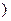 上是增函数.
上是增函数.