(本题满分12分)
投掷飞碟的游戏中，飞碟投入红袋记2分，投入蓝袋记1分，未投入袋记0分.现知某人在以前投掷1000次的试验中，有500次入红袋，250次入蓝袋，其余不能入袋
（1）求该人在4次投掷中恰有三次投入红袋的概率;
（2） 求该人两次投掷后得分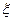
的分布列和数学期望.
，
，若
，求
的取值范围．
，
，
，
，
，求：
的
值；
，
的
的
，
，且
，求
，
的值
，
，
，求
的值．
，
，
求
的值.推荐套卷
(本题满分12分)
投掷飞碟的游戏中，飞碟投入红袋记2分，投入蓝袋记1分，未投入袋记0分.现知某人在以前投掷1000次的试验中，有500次入红袋，250次入蓝袋，其余不能入袋
（1）求该人在4次投掷中恰有三次投入红袋的概率;
（2） 求该人两次投掷后得分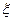的分布列和数学期望.
粤公网安备 44130202000953号