假设关于某设备使用年限x(年)和所支出的维修费用y(万元)有如下统计资料:
 |
2 |
3 |
4 |
5 |
6 |
 |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
若由资料知,y对x呈线性相关关系,试求:
(Ⅰ)请画出上表数据的散点图;
(Ⅱ)请根据上表提供的数据,求出y关于x的线性回归方程 ;
;
(Ⅲ)估计使用年限为10年时,维修费用约是多少?
( )
)
相关知识点
推荐套卷
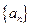 满足对任意的
满足对任意的 ,都有
,都有 ,且
,且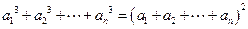 .(1)求
.(1)求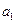 ,
,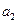 的值;(2)求数列
的值;(2)求数列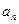 ;(3)设数列
;(3)设数列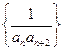 的前
的前 项和为
项和为 ,不等式
,不等式 对任意的正整数
对任意的正整数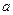 的取值范围.
的取值范围.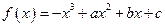 在
在 上是减函数,在
上是减函数,在 上是增函数,函数
上是增函数,函数 在
在 上有三个零点,且1是其中一个零点.(1)求
上有三个零点,且1是其中一个零点.(1)求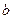 的值;(2)求
的值;(2)求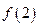 的取值范围;(3)试探究直线
的取值范围;(3)试探究直线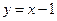 与函数
与函数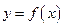 的图像交点个数的情况,并说明理由.
的图像交点个数的情况,并说明理由. 粤公网安备 44130202000953号
粤公网安备 44130202000953号