(本题满分14分)．如图所示，四棱锥P－ABCD的底面积ABCD是边长为1的菱形，
∠BCD＝60°，E是CD的中点，PA⊥底面积ABCD，PA＝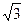
.
(Ⅰ)证明：平面PBE⊥平面PAB；
(Ⅱ) 过PC中点F作FH//平面PBD, FH交平面ABCD 于H点，判定H点位于平面ABCD的那个具体位置？（无须证明）
（Ⅲ）求二面角A－BE－P的大小.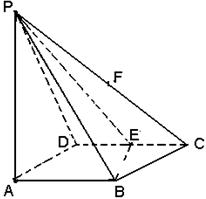 
化为
进制的数.
和
的最大公约数，并用更相减损术检验所得结果.
+
+
+…+
的值的流程图.推荐套卷
(本题满分14分)．如图所示，四棱锥P－ABCD的底面积ABCD是边长为1的菱形，
∠BCD＝60°，E是CD的中点，PA⊥底面积ABCD，PA＝.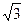
(Ⅰ)证明：平面PBE⊥平面PAB；
(Ⅱ) 过PC中点F作FH//平面PBD, FH交平面ABCD 于H点，判定H点位于平面ABCD的那个具体位置？（无须证明）
（Ⅲ）求二面角A－BE－P的大小.
粤公网安备 44130202000953号