（本小题满分12分）函数f（x）对任意的实数m,n，有f（m+n）=f（m）+f（n），当x＞0时，有f（x）＞0。
①求证：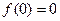
②求证：f（x）在（－∞，+∞）上为增函数．
③若f（1）=1，解不等式f（4x－2x）＜2．
的导数。
的某一切线与直线
平行，求切点坐标。
是函数
的切线，求
的值。
，求
时
的值。
，利用定义求
。推荐套卷
（本小题满分12分）函数f（x）对任意的实数m,n，有f（m+n）=f（m）+f（n），当x＞0时，有f（x）＞0。
①求证：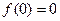
②求证：f（x）在（－∞，+∞）上为增函数．
③若f（1）=1，解不等式f（4x－2x）＜2．
粤公网安备 44130202000953号