（本小题满分12分）
如图,三定点A(2,1),B(0,－1),C(－2,1); 三 动点D,E,M满足="t," =" t" ,
="t" , t∈[0,1].
(Ⅰ) 求动直线DE斜率的变化范围;
(Ⅱ) 求动点M的轨迹方程.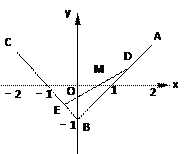
相关试题
中，底面
是边长为
的菱形，
,
底面
,
为
的中点，
为
的中点.
平面
；
与
所成角的大小；
时，其前n项和满足
.
，数列{bn}的前n项和为
，求
为常数）．
时，
的最小值为– 2 ，求a的值．
(
为实常数) ．
时，求函数
在
上的最大值及相应的
值；
时，讨论方程
根的个数．
，且对任意的
，都有
，求实数a的取值范围.
的左右两焦点分别为
，
是椭圆上一点，且在
轴上方，
．
的取值范围；
的圆
的截
轴的线段长为6，求椭圆的方程；
上任一点
引圆
．试探究直线
是否过定点？若过定点，请求出该定点；否则，请说明理由．推荐套卷
（本小题满分12分）
如图,三定点A(2,1),B(0,－1),C(－2,1); 三 动点D,E,M满足="t," =" t" ,
="t" , t∈[0,1].
(Ⅰ) 求动直线DE斜率的变化范围;
(Ⅱ) 求动点M的轨迹方程.
粤公网安备 44130202000953号