（本小题满分14分）
如图，在直三棱柱ABC—A1B1C1中，∠
ABC=90°，BC=2，AB=4，CC1=4，E在BB1上，且EB1=1，D、F分别为CC1、A1C1的中点。
（1）求证：B1D⊥平面ABD；
（2）求异面直线BD与EF所成的角；
（3）求点F到平面ABD的距离。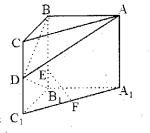
,求
的值．
，问方程
在区间[－1，0]内是否有
在(0,1)内恰有一解，求实数
的取值范围．
，求
的值.
终边上一点
的坐标为
，
；
求
的值。推荐套卷
（本小题满分14分）
如图，在直三棱柱ABC—A1B1C1中，∠ABC=90°，BC=2，AB=4，CC1=4，E在BB1上，且EB1=1，D、F分别为CC1、A1C1的中点。
（1）求证：B1D⊥平面ABD；
（2）求异面直线BD与EF所成的角；
（3）求点F到平面ABD的距离。
粤公网安备 44130202000953号